By Dr. Matsakis
Tau Day: Are Two Pies Better than One?
Every geek knows that March 14 is Pi Day, because 3.14 is a 3-digit approximation of pi (π). Of course, π is an irrational number, so you can’t write it down without using an infinite number of digits. [1] Those digits start out as 3.14159265358979323, but they just keep on going. When I last checked, π was known to 31 trillion digits. [2] That’s just about what our national debt should be at the end of this year. Some people think they have found a message from our creator in all those numbers. The sum of the first 144 digits is 666, the sign of the devil. But maybe it wouldn’t be that way if we didn’t have ten fingers.
Another approach is to simplify the problem. In 1897, based on poor mathematical advice, Indiana’s state legislature set π to equal 3.2. [3] That would have made Pi Day March 2, had it stuck. But it didn’t, so we now have the real Pi Day to celebrate the mysteries of the mathematical universe and to show off our erudition and our baking ability by bringing pies to work, school, and social gatherings.
But is all this attention misplaced? Michael Hartle says π is only half the story. [4] That’s because in almost every formula of math and physics where you see π, it is part of 2. So Hartle multiplied π by 2, and called it tau, which is the Greek letter τ. He gives talks to other geeks and says τ is the magical number we should teach our children. He’s already taught τ to Python programmers, who can get it from the math library with the command “from math import tau.”
If Hartle is right, then we should be celebrating Tau Day on June 28 (6/28). And he might be right. As he points out, many great mathematicians of yesteryear, like Euler and Archimedes, used the equivalent of τ in their work. See also the back of a t-shirt I designed:
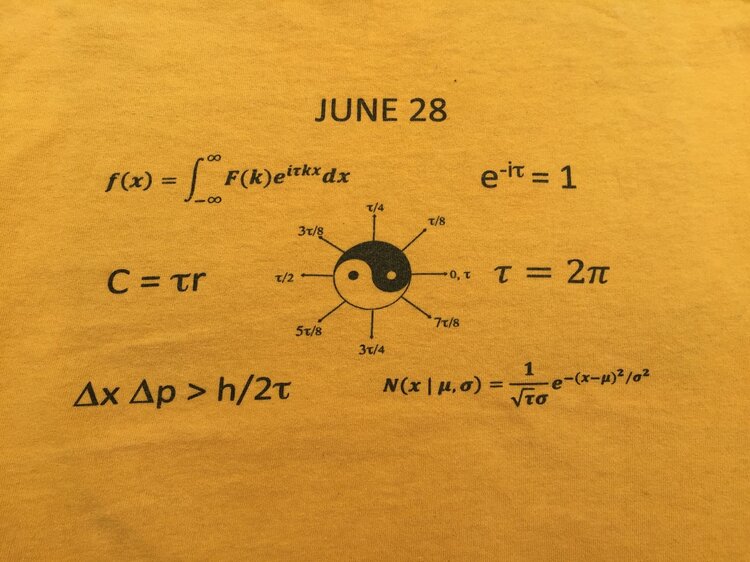Those are all fundamental formulas of mathematics and physics written to save ink by replacing 2π with τ. Starting clockwise from the top right, we see a very strange conglomeration of bizarre numbers equaling 1. The “e” in there is the natural base for logarithms, which is also an irrational number, approximately 2.718. And “i” is the imaginary number equal to the square root of -1. Can that formula also be a message from our creator? I don’t know, but skipping past the definition of τ, we find Gauss’s formula for how probabilities are computed on the bottom right. To the left is Heisenberg’s uncertainty principle, which lays the foundation of quantum mechanics by saying that the uncertainty of a particle’s position times the uncertainty of its momentum is always greater than a certain amount determined by Planck’s constant. Next, we come to the formula for the circumference of a circle, C = τr, which you would know as C = 2πr. And finally, on the top left, we come to Fourier transforms, which are a way you can express any formula as a sum of oscillating waves. I didn’t include Einstein’s field equations, but they have an 8 in front of the π. I could explain why 4τ is more rational, but since Einstein’s birthday is March 14, it would be more respectful to leave that one alone.
So on June 28, the Masterclock team will enjoy two pies—and the prize goes to whoever can find the secret message hidden in 6.2831853071819586…
Footnotes
[1] An irrational number is one that can’t be expressed as the ratio of two integers. For example, .14 is rational because it is 14/100. Pi is both an irrational and a transcendental number, which means it can never be the root of a non-zero polynomial with rational coefficients. An example of an irrational number that is not transcendental is √2 which is the solution to the polynomial equation x^2 - 2 = 0. When Pythagoras discovered irrational numbers existed, he made it a secret upon pain of death.
[4] See https://tauday.com.
About Dr. Demetrios Matsakis
Dr. Demetrios Matsakis attended MIT as an undergraduate and received his PhD in physics from UC Berkeley, where he studied under the inventor of the maser and laser; and built specialized ones in order to observe interstellar dust clouds where stars are born. His first job was at the U.S. Naval Observatory, building water vapor radiometers and doing interferometry to observe quasars and galaxies at the edge of the observable universe. After developing an interest in clocks, Dr. Matsakis would spend the next 25 years working hands on with most aspects of timekeeping – from clock construction, to running the USNO’s Time Service Department, to international policy. He has published over 150 papers and counting, but gets equal enjoyment out of beta-testing his personal ensemble of Masterclock products.
Latest Scientific Editorial by Dr. Demetrios MatsakisIntroducing Modern Timekeeping & Time Transfer
